
Groups—such as clusters of points or communities of nodes—are fundamental when addressing various data mining tasks. In temporal data, the predominant approach for characterizing group evolution has been through the identification of “events”. However, the events usually described in the literature, e.g., shrinks/growths, splits/merges, are often arbitrarily defined, creating a gap between such theoretical/predefined types and real-data group observations. Moving beyond existing taxonomies, we think of events as “archetypes” characterized by a unique combination of quantitative dimensions that we call “facets”. Group dynamics are defined by their position within the facet space, where archetypal events occupy extremities. Thus, rather than enforcing strict event types, our approach can allow for hybrid descriptions of dynamics involving group proximity to multiple archetypes. We apply our framework to evolving groups from several face-to-face interaction datasets, showing it enables richer, more reliable characterization of group dynamics with respect to state-of-the-art methods, especially when the groups are subject to complex relationships. Our approach also offers intuitive solutions to common tasks related to dynamic group analysis, such as choosing an appropriate aggregation scale, quantifying partition stability, and evaluating event quality.
Avoid common mistakes on your manuscript.
Unsupervised learning, such as clustering and community detection, involves identifying collections of elements that share some form of similarities. Clustering methods identify groups of observations or entities, based on their proximity across multi-dimensional features (MacQueen et al., 1967). Community detection aims to describe the mesoscale dimension of a complex network, grouping nodes that share similar structural behaviour (Fortunato & Hric, 2016). Such groups are often referred to as clusters in data mining-related fields, and communities in complex network analysis. In the remainder of this article, we will use the generic term of “group”. Groups are fundamental when addressing a wide variety of data mining and network science-related questions, such as segmenting customers to improve recommender systems or identifying echo chambers in social media to de-polarize online discussions.
Often, real data are stored as streams or sequences of multi-dimensional points (Zubaroğlu & Atalay, 2021) or links (Rossetti & Cazabet, 2018) such that the formation and evolution of groups can be tracked quantitatively over time. The challenge of identifying evolving groups has emerged as a distinct subfield in many areas; see spatiotemporal data clustering (Ansari et al., 2020; Kisilevich et al., 2010), data stream clustering (Zubaroğlu & Atalay, 2021), and dynamic community detection (Rossetti & Cazabet, 2018).
A key concept specific to dynamic group evolution is the notion of event (Bródka et al., 2013; Lughofer, 2012; Palla et al., 2007; Rossetti & Cazabet, 2018). Intuitively, an event is a temporal occurrence involving changes that can be measured and analyzed for a group or a set of groups. A change can be the growth or the shrinking of a group, or the merging of two groups into a larger one. These events have been defined in the literature a priori (Asur et al., 2009; Brodka et al., 2009; Bródka et al., 2013; Greene et al., 2010; Palla et al., 2007), based on what one wishes to extract from the data, and not from the reality of group evolution observed in data. As a consequence, in most datasets we are confronted with a gap between theoretical events such as “merge” or “growth”, and what one actually observes. Most group evolution seems indeed more complex, frequently being a combination of those artificial categories.
In this work, rather than using those strict event definitions, we consider them as “archetypes”, i.e., typical examples of a category conveying its most salient features (Rosch, 1975), while real events can exhibit features from multiple of these archetypes. To tackle this more complex definition, we propose a quantitative definition of event archetypes as a unique combination of three constitutive dimensions called facets. Each event is thus defined by a position in this 3-dimensional space, in which usual events occupy an extremity. Following (Bovet et al., 2022), we consider backward and forward perspectives to study the temporal evolution of a target group.
The rest of the paper is organized as follows. Section 2 sums up the essential literature about temporal clustering across different domains and the need to build taxonomies to describe the life cycles of groups. Section 3 describes our framework for characterizing the temporal evolution of target groups as weighted approximations of archetypal events. Section 4 introduces an experimental setting to test our methodology in real-world data. Finally, Sect. 5 concludes the work by discussing its potentiality and limits.
Data stream clustering, temporal clustering, and dynamic community detection are active research topics, and many algorithms have been proposed to identify time-varying groups (Rossetti & Cazabet, 2018; Kisilevich et al., 2010; Ansari et al., 2020; Zubaroğlu & Atalay, 2021). However, most of these works do not address the question of group events. Indeed, dynamic grouping methods often yield their groupings in one of two forms, as illustrated in Fig. 1: (i) The method might only focus on the groups found at each step, for instance ensuring the stability of these groups in time. In that case, we know what are the groups at t and at \(t+1\) , but there is no information in the relation between groups in t and in \(t+1\) (Fig. 1a); or (ii) each group is a set of (entity/time) pairs, i.e., a group exists over multiple timesteps, potentially allowing entities to join and leave the group along time (Fig. 1b). However, none of these representations explicit what the events undergone by evolving groups are. In this work, we will consider starting from a sequence of temporally ordered observations, i.e., snapshots, and sets of partitions on these snapshots, obtained from an existing method—or possibly, from a ground truth—as illustrated in Fig. 1a. The task consists in characterizing the nature of the relation between groups at time t and at time \(t+1\) , in the form of events.
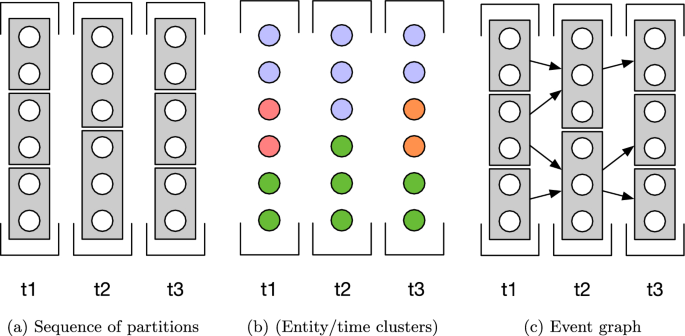
The earliest attempts to define events on groups can be found in Kalnis et al. (2005) and Hopcroft et al. (2004), with the objective to identify Continuation events, i.e., to define that group \(c_1\) at time \(t_1\) should be considered as the same group as \(c_2\) at time \(t_2\) , a process also known as matching groups. Kalnis et al. (2005) proposed to match groups if (i) they are adjacent, and (ii) their Jaccard coefficient is above a threshold \(\tau\) . Given \(c_t\) and \(c_\) , namely two groups observed over temporally adjacent snapshots, if \(\frac<|c_t \, \cap \, c_|><|c_t \, \cup \, c_|> \ge \tau\) , the two groups are the same. \(\tau\) is a parameter considering the “integrity” of a group, and it indicates the minimum overlap threshold required for two groups to be considered the same. Similarly, to identify a Continuation event in dynamic networks, Hopcroft et al. (2004) defined a match function as follows: \(match(c_t,c_)=Min(\frac<|c_t \, \cap \, c_|><|c_t|>, \frac<|c_t \, \cap \, c_|><|c_|>)\) ; then, if \(match(c_t,c_) \ge \tau\) , the two groups are matched. However, without particular constraints on the value of \(\tau\) , there is no guarantee that a group is matched to a single group in the following step. The process thus naturally creates an event graph (Rossetti & Cazabet, 2018), as illustrated in Fig. 1c. Greene et al. (2010) were the first to formalize this event graph and to propose to use it to define typical events. A group having an out-degree of two or more is labeled as undergoing a Split event. An in-degree of two or more is a Merge . In/Out degrees of zero respectively lead to Birth and Death events. Finally, the authors mention that Contraction , Expansion , and Continuation all correspond to the same graph setting, but can be distinguished by adding size thresholds. It is worth noting though that despite its elegance and apparent simplicity, this approach creates complex situations: a group \((t_1,c_1)\) can be matched to two groups \((t_2,c_2)\) , \((t_2,c_3)\) , but one of these groups might itself have an in-degree of more than one, thus being a merge of \((t_1,c_1)\) and \((t_1,c_4)\) . These situations are not discussed in the article of Greene et al. (2010).
This merge-split ambiguity can be solved by adding some additional constraints, such as in Asur et al. (2009), in which an event is categorized as a merge if the following three conditions hold: (i) \(\frac<|(c^i_t \, \cup \, c^j_t) \, \cap \, c_|>
Bródka et al. (2013) aimed to define as many events as possible by proposing a methodology for detecting group evolution, namely the Group Evolution Discovery (GED) framework. They introduce a measure to quantify the inclusion of one group into another based on both group sizes and a centrality measure called Social Position (SP) (Brodka et al., 2009), namely a function calculating how much a node is important in a group based on the importance of its neighbors. The group events are defined on the basis of a decision tree that assigns an event type to a pair of groups given some thresholds on sizes and inclusion values. Similarly to GED, Gliwa et al. (2012) introduced an algorithm for Stable Group Changes Identification (SGCI), where complex events such as merge, split, and split+merge (a split of the original group and the joining of many groups into successor groups) are associated to groups that have been found stable in neighboring time steps. The stability depends on a match function defined as \(Max(\frac<|c_t \, \cap \, c_
To complete the overview of the analysis of complex event types in data mining- and network science-related tasks, it is worth mentioning works moving beyond merely identifying group events, but also employing them to predict the future evolution of a system. Typically, this subject has been modeled as a machine learning task, commonly in the form of a classification problem, where a set of features is extracted from the events and used to predict an event type (Saganowski, 2015). The events defined for building the training sets can be obtained from the methods previously described. In Saganowski (2015), events are described through the previously mentioned GED (Bródka et al., 2013) and SGCI (Gliwa et al., 2012) algorithms. Group features used for prediction are size, density, and the sum/average/min/max of aggregated group members’ features, such as node degree and other centralities measures. Other works exploit forecasting methods for time series, predicting how the features extracted from the events will change in the following time period İlhan, and Öğüdücü, (2015). The latest directions of research are starting to focus on the behavior and prediction of individual entities. For instance, Tsoukanara et al. (2021) proposed to predict, using node embedding methods, beyond event types, whether a specific node stays in the same group, moves to another group, or drops out of the dataset.
Existing event detection methods suffer from some limitations, which might explain their limited use in practice.
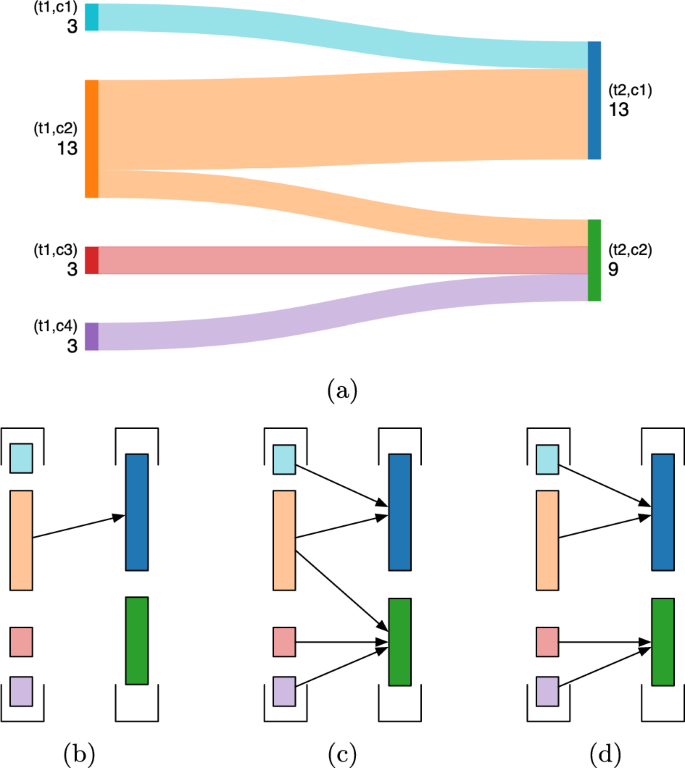
The first limit is the sensibility to the fixed threshold \(\tau\) . Choosing a large threshold will cause many groups to die and be born at each step, while a low one will create complex events involving multiple groups from t and from \(t+1\) together, as illustrated in Fig. 2. Choosing this parameter thus strongly affects the results. Although some authors have proposed to use a dynamic threshold (Mall et al., 2015), the problem of their arbitrary values and binary categorization remains present.
Another limit is the discrepancy between having a list of well-defined events—Continuation, Birth, Death, Merge, Split, Expansion, Contraction—and the more complex reality of real situations, as illustrated in Fig. 2a. We can observe that from the point of view of (t1, c2), the event can be interpreted as either a split or a continuation, with a minor number of entities leaving the group. From the point of view of (t2, c1), we can again interpret what is happening as a merge or as a continuation, depending on the threshold fixing what quantity of entities is considered a negligible fraction. An even more ambiguous case is the relation between (t1, c2) and (t2, c2) since a minority fraction of entities leaves the first, but they represent a large fraction of the newly formed one. We can formalize the difficulties encountered by those previous methods by their definition of an event, which involves a set of groups from two adjacent timesteps, without a notion of direction. Instead, we argue that a split, for instance, only makes sense when following the direction of time, while a merge is characterized by considering the opposite direction. Thus, in the case of Fig. 2c, we must extract a split from the point of view of (t1,c2), in the direction of time, and a merge from the point of view of (t2,c1), in the reverse direction.
Finally, a last limit of those approaches comes from their disregarding of the distinction between entities moving between groups, and those joining or leaving the system altogether. As an example, a death event might actually correspond to multiple situations: (i) all the entities composing the group might have left the studied system, (ii) entities might have split up and joined other groups. Conversely, a newborn group might be formed from entities joining the system, or from individual entities coming from multiple sources. Intuitively, these situations are different, but existing events do not distinguish them. This limit had already been discussed in Pereira et al. (2021), that introduced a taxonomy including for instance sub-categories for death events, namely death-vanish and death-absorb.
In the literature, events are defined as mutually exclusive categories. In the event-graph representation, the in-degree of a group allows one to distinguish between a merge ( \(k^\ge 2\) ), a birth ( \(k^=0\) ), and a continuation ( \(k^=1\) ). Instead, our approach first describes quantitatively the nature of an event using scores called event facets.
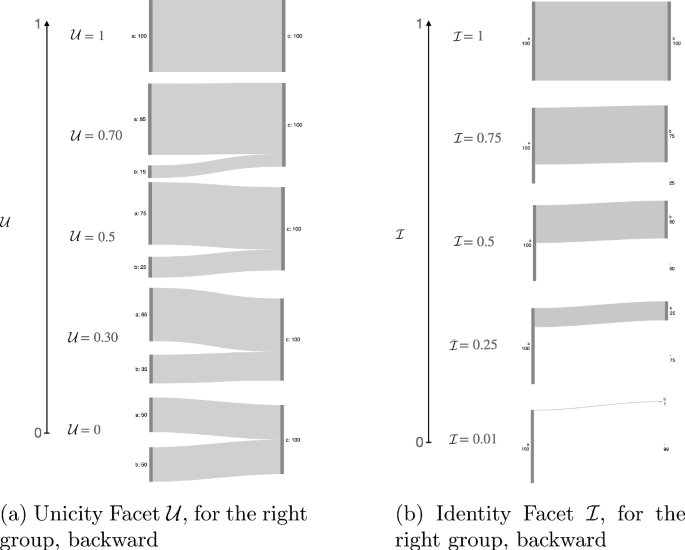
The first facet is called the Unicity Facet. In the forward perspective, it measures if the entities tend to stay together in a single group, or are disseminated in multiple destination ones, with no dominant one. Conversely, in the backward perspective, it measures if all the entities come from a single source or multiple ones. The unicity facet can be understood as a continuous transition between \(\frac>>=1\) and \(\frac>>=\ge 2\) in the event graph formalism. Figure 3a illustrates this facet in the backward perspective. For a target set X, composed of subsets \(\mathcal \) , each subset corresponding to a different related set, the Unicity of X is defined as the difference between the fraction (relative size) of the elements in the two largest subsets in \(\mathcal \) .
(Unicity Facet) Let X be the target set, and \(\mathcal = [R_1,\dots , R_<|\mathcal |>]\) be the related set, ordered in decreasing order of intersection size with X, i.e., \(\forall _ j>,|R_i \cap X|\ge |R_j \cap X|\) .
The Unicity Facet is defined as:
$$\beginThis score guarantees that a large value corresponds to (e.g., in the backward perspective) having one dominating source, and reciprocally, that having a dominating source leads to a high score. Conversely, having a low score corresponds to having no dominating unique source, and having no dominating source leads to a low score.
Note that several diversity indices exist in the literature, such as Gini’s, Herfindahl’s, and normalized Shannon diversity indices, that yield similar results on the example of Fig. 3. However, they do not correspond to our needs, since they do not measure the concentration of values in the dominant source, but rather the concentration in a small fraction of all the sources. This means that these indices can yield low values even in the case of clear merges, or in the case of a large number of different sources. Dominance scores such as the Berger-Parker index, suffer from other limits. The shortcomings of all those scores for Unicity are detailed in Appendix 1.
When no set contributes to X, i.e., all elements \(x \in X\) are observed for the first time, it can be thought of as if all elements came from a single set existing before our observation period. We thus assign \(\mathcal = 1\) in that case. Note that apart from this specific situation, elements observed for the first (resp. last) time play no role in Unicity. Indeed, their presence is taken into account by another facet.
An aspect of events that is not directly tackled by existing literature is the question of the preservation of groups’ identity. The term is taken as a parallel with social groups, such as for instance a political party. The group itself can be considered to have an identity, and if too many individuals leave the group, that identity might be lost. The Identity facet measures how much of the identity is transferred by/to the target group. Taking as an example the backward perspective, let us consider a group g, which receives all of its nodes from a group \(g_\) . The Identity facet measures if the elements of g represent a large fraction of the nodes of \(g_\) , or only a small fraction of them. The facet thus ranges from 0 to 1, 1 if all the nodes of \(g_\) joined g— thus, the nodes are considered to come with the identity of their group of origin— and tends towards 0 as the nodes joining g represent a smaller fraction of \(g_\) . Figure 3b illustrates this facet in the backward perspective.
(Identity Facet)
As an illustrative example, assume that a single set of 10 elements, R, provides elements to X with two alternative scenarios: (a) it provides a single element, and (b) it provides 9 out of 10 elements. In the former scenario, the contribution \(\mathcal \) will approach 0; in the latter, it will approach 1 (reaching those extreme values only when none or all elements of \(\mathcal \) are present in X).
Note that \(\mathcal =0\) if there is no related set: in that case, the group identity is completely lost (forward) or completely new (backward).
The outflow facet measures the fraction of the group elements that (i) just joined the system in the backward perspective, or (ii) left the system, in the forward perspective. The Outflow facet can be understood as a continuous transition between \(\frac>>=0\) and \(\frac>>=1\) in the event graph formalism, i.e., a birth (resp., death) and a continuation. The facet thus ranges from 0—all elements of the group were already present (resp., remain) in the system—to 1 — all elements of the group are new (resp., are not present in the next timestep).
( Outflow Facet)
$$\begin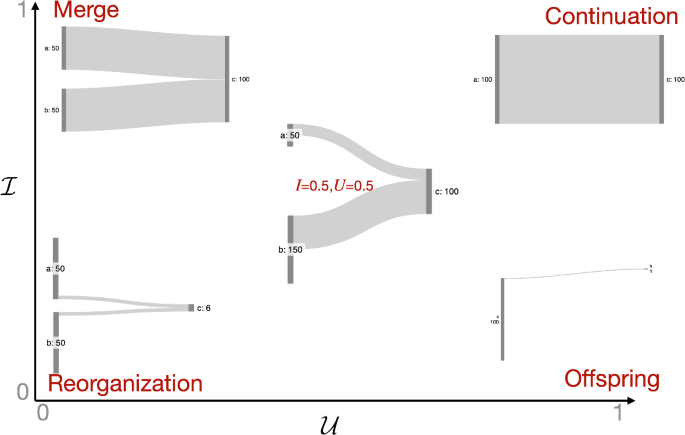
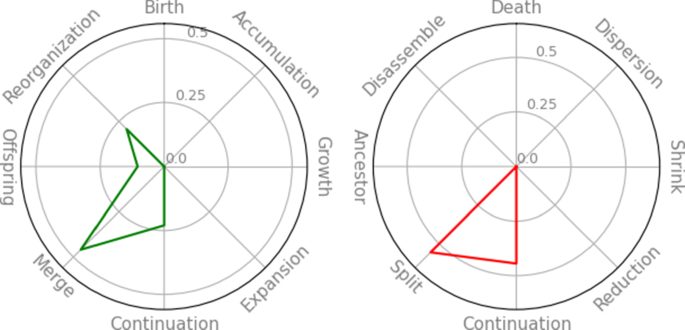
The facets introduced above describe intuitive quantities that can be used to characterize a group with respect to its evolutionary history, either past or future. Going further, the evolutionary processes that outline a group’s life cycle can be seen as a series of archetypal events that the cluster undergoes. Here, we introduce the possibility of quantifying how much a group and its immediate predecessors/successors approximate some archetypal transformations, by combining facet scores into Event weights. Figure 4 illustrates the relation between two of these facets and event archetypes, some of them common in the literature (Merge, Continuation), some others being new (Reorganization, Offspring), but emerging naturally from our definitions.
We acknowledge that real-world evolutionary events are rarely found in their “pure” or “archetypal” form, often manifesting as complex and hybrid processes, often mired in messiness. As such, it is relevant to characterize these processes as composite, measuring the extent to which they approximate (one or more) “pure” events.
Under the backward perspective, we can do so with the following event weights.
(Backward Event Weights) Let X be the target set and \(\mathcal \) be the set of related groups such that X evolves from \(\mathcal \) . Backward event weights quantify the extent to which X’s evolution from \(\mathcal \) approximates one of the following transformations:
$$\begin
Birth events are characterized by a high number of joining elements that compose a set X, thus, a pure, archetypal Birth is found when the outflow \(\mathcal \) is maximized. Theoretically, looking at the past to identify a birth is irrelevant since the appearance of new elements is unrelated to the incoming flow. In real-world events, however, some fluctuating elements in R can also join such newborn sets. The Unicity facet \(\mathcal \) of the few elements joining a newborn set lets us further distinguish between a pure Birth and an Accumulation , i.e., a birth from subsets – minimizing \(\mathcal \) .
When the Identity facet is maximized in the absence of new elements, we characterize a Continuation , if Unicity \(\mathcal \) is maximized, or a Merge , if \(\mathcal \) is minimized. Continuation events identify elements from a single set that are found together (i.e., in the same set) in the next timestamp. Merge events identify the case where two or more sets of similar size join to form a single set in the next timestamp.
When the Identity facet is low, and in the absence of new elements, we can witness an Offspring or a Reorganization , depending on the Unicity. A pure, archetypal Offspring is observed when \(\mathcal \) is maximized, meaning that a small portion of a single origin set is found in the target set. A Reorganization occurs when \(\mathcal \) is minimized, meaning the target set comprises small portions of several contributing sets.
When the backward Unicity is maximized in the presence of many new nodes ( \(\mathcal \) large), we can witness a Growth . A pure, archetypal Growth is a single set that expands over the next timestamp, thus it is found by maximizing all three facets: Unicity (Single source), Identity (all the source), Outflow (numerous new nodes). If \(\mathcal \) is minimized, we call the archetype an Expansion , i.e., similar to a Growth but from several contributing subsets. It should be noted that when \(\mathcal =1\) , then by definition \(\mathcal =1\) and \(\mathcal =0\) , i.e., we are in a Birth situation. This means that archetypes Accumulation , Growth , and Expansion can never reach a value of 1, but can only get close to this maximal value when a majority of nodes are new, but some come from existing groups.
Similarly to Definition 4, other events can be described by adopting the forward perspective.
( Forward Event Weights) Let X be the target set and \(\mathcal \) be the set of related groups such that X evolves into \(\mathcal \) . Forward event weights quantify the extent to which X’s evolution into \(\mathcal \) approximates one of the following transformations:
$$\begin
The main difference with respect to the events in Definition 4 relates to the meaning of \(\mathcal \) . From the backward perspective, we compare the target set with the partition in the previous timestamp, so the elements quantified by the Outflow facet are “new”, i.e., they are not present in the previous timestamp. Contrarily, from the forward perspective, we compare the target set with the partition in the next timestamp, so the elements quantified by the Outflow Facet are “dead”, i.e., they are not present in the next timestamp. Thus the equation for Death is the same as for Birth . A similar situation is found with Accumulation and Dispersion , Merge and Split , Offspring and Ancestor , Reorganization and Disassemble , Growth and Shrink , Expansion and Reduction . The Continuation event, instead, is undirected, meaning that it is measured in the same way regardless of the temporal direction.
Finally, one might be interested in studying events that are closer to their archetype with respect to others, for instance, to separate them from more complex events. To distinguish between less and more pure transformations, we introduce the Event Typicality Index, defined as follows:
Let \(E_X\) be the set of Backward or Forward Event Weights computed for set X. The Event Typicality Index \(\mathcal \) is computed as the maximum value among the event weights. Formally:
$$\beginEvents corresponding perfectly to archetypes thus have \(\mathcal =1\) .
Events as they are usually defined in the literature, such as Rossetti and Cazabet (2018), are bidirectional in the sense that they are defined without a sense of direction. The exceptions are Birth and Death, which match our definitions, since they involve groups in only one timestep. For the others, we can describe these bidirectional events using our formalism as a combination of forward and backward events, as follows:
In this section, we apply the proposed framework to analyze the evolution of groups from real-world data.
We leverage the datasets from the SocioPatterns project, Footnote 1 more precisely the Hospital (Vanhems et al., 2013), Primary School (Stehlé et al., 2011), and High-School (Mastrandrea et al., 2015) datasets. All of them correspond to face-to-face interactions collected via RFID sensors over 4, 2, and 7 days, respectively. They are frequently used in the context of dynamic network analysis, as they allow the consideration of multiple aggregation scales, have a reasonable size to be studied in detail, and undergo dynamics over the studied periods.
As a pre-processing, we first aggregate the data into a series of static networks, using a chosen time scale (hour, day, etc.). We then apply a community detection algorithm, namely the Louvain modularity maximization approach (Blondel et al., 2008). Louvain is a non-deterministic algorithm, meaning that it may return different partitions over multiple runs. We perform some sanity checks on running Louvain on these datasets, and detail them in Appendix 2. This process yields sequences of node partitions, i.e., sets of sets, that constitute the input to our framework.
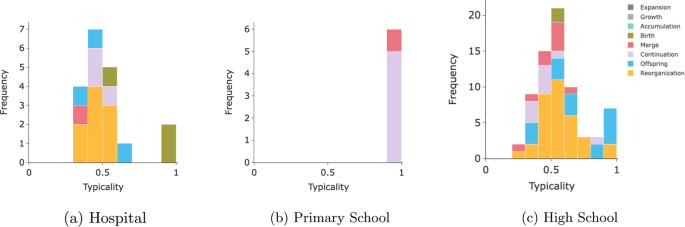
In Sect. 3.4, we defined the typicality of an event as the maximal event score for that event in a particular direction. We can leverage this information to describe system-wide the distribution of event types and typicality in a network. In Fig. 5, we plot this distribution for the three datasets at the daily aggregation level. The results are coherent with what we observed for the stability, with the primary school dataset composed mostly of archetype Continuation and Merge , while the other datasets, mostly unstable, exhibit poorly defined events, at the exception of a few Birth and Offspring .
Comparing the quality of events detected using our approach with those found by previous methods is difficult, due to (i) the absence of external ground truth, and (ii) the difference in nature between events found by previous methods and those produced by our approach. Therefore, we illustrate the interest of our formalism in case studies.
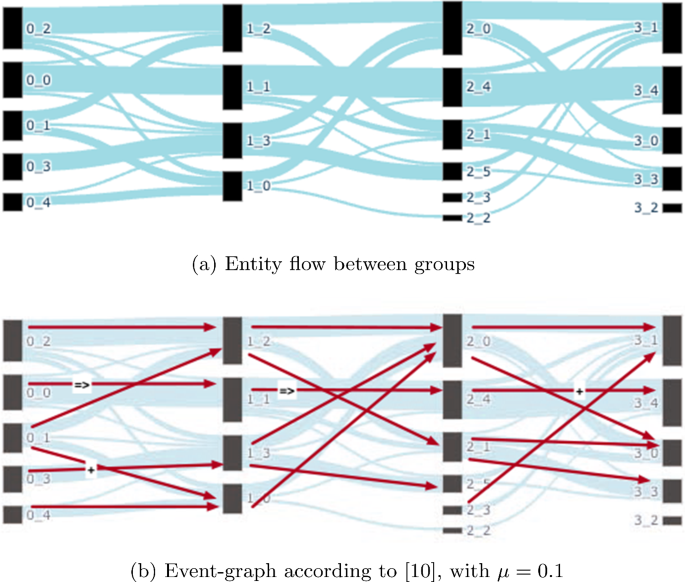
In the following, we compare our framework with the event graph formalism by Greene et al. (2010), and the framework by Asur et al. (2009). on the Hospital Dataset, using a daily aggregation window. Daily aggregation seems intuitively reasonable on SocioPatterns datasets, and has commonly been used in the literature. We have seen from Table 2 that it leads to rather unstable partitions for the Hospital dataset. Figure 6a represents the flow for the four days. We observe that the relations between groups are complex, and that assigning archetypes to events does not seem obvious.
Figure 6b represents the event graph obtained from Greene et al. (2010) at the \(\mu =0.1\) threshold, observed to work best by the authors. We observe that in most cases, the events recognized are rather logical: 0_2 and 2_0 being Merge events, 0_1 and 1_3 being Split events, etc. Only 2 events are Continuation , and 2 others are Growth . However, in several other cases, the events obtained are more disputable. Is there no relation between 1_0 and 2_2 ? Is 1_3 really a growth from 0_3 ? Why 0_2 is not a split? These limits are consequences of the research of archetypes only, without taking into account the multiple facets of events. Another limit is that most events are intertwined split-and-merge, i.e., out-going branches of Split s form in-going branches of Merge s. The interpretation of such events thus becomes difficult: it seems abusive to say that, for instance, 3_0 is a merge of 2_0 and 2_1 , while both these groups are subject to Split , and only minor fragments of them join into 3_0 .
Using the framework from Asur et al. (2009) leads to an even more unsatisfactory result, since it yields only six recognized events: two Merge s, two Split s, and two Birth s. Indeed, this framework is very conservative in its definition of events, and most flows are too complex to be recognized as such.
Using our framework, we obtain a richer description of events. We first can consider the typicality of events to identify the closest to archetypes. For instance, the 3 highest forward- Continuation are 0_0,1_1,2_4 , corresponding to the same group of people continuing in the same group, although not in perfect Continuation . Similarly, the three highest Split scores are 1_3,2_1,2_0 . We observe that these descriptions are compatible with the description obtained from Greene et al. (2010). However, our framework offers more details. For instance, the forward Continuation of 0_0 also has, in decreasing magnitude, Ancestor , Split and Disassemble facets. Indeed, some of its components join other groups, while its components represent only 9 out of 15 elements in 1_1 , making it far from an archetypal Continuation .
In another example, we focus on an event that seems unconvincing according to Greene et al. (2010), 1_3 seen as a growth from 0_3 . We provide the complete facets of 1_3-backward :
We observe that the dominant facet is reorganization , since it is composed of multiple minor parts of previous groups. It also has some elements of Merge , Offspring , and Continuation , which is due to the complexity of receiving a large fraction of its components from the bulk of a single group, while the rest are minor fragments from various other groups.
From this example, we see that when the groups are subject to complex relationships, state-of-the-art approaches yield potentially misleading results, while the richer description of our framework allows a better characterization of group evolution.
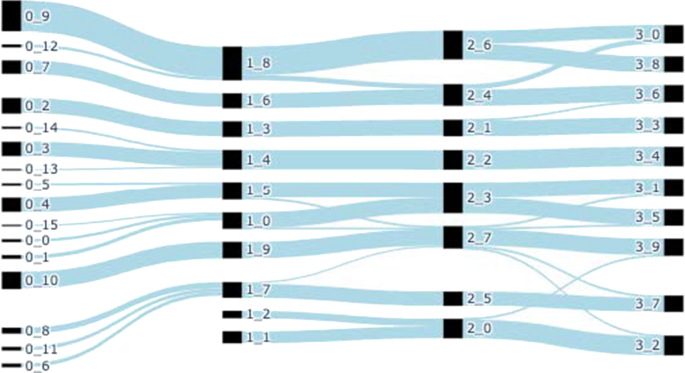
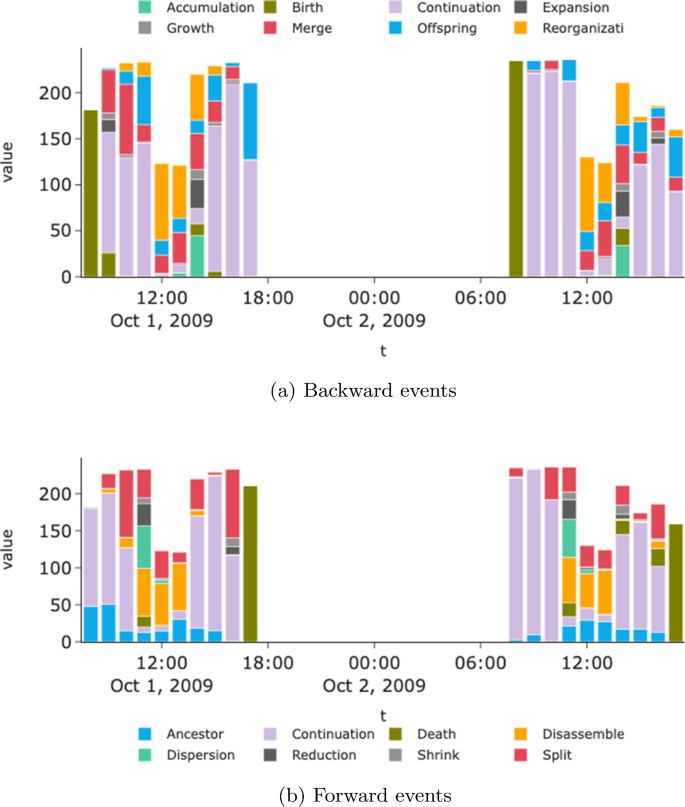
We then focus on the Primary School dataset, at the hourly aggregation timescale. We have seen from Table 2 that it is the most stable aggregation step, if we ignore the 1-minute aggregation steps that yield very small groups, and the PS 1-day aggregation window, which contains nearly only perfect Continuation events as seen in Fig. 5.
We first focus on the details of the flow during the first 4 h and plot the details in Fig. 7. We observe that events seem indeed much easier to characterize than in the previous case.
Many events are recognized as pure Continuation by all three frameworks, such as ( 0_2 \(\rightarrow\) 1_3 ),( 0_10 \(\rightarrow\) 1_9 ),( 1_3 \(\rightarrow\) 2_1 ), etc. All frameworks also agree on Birth events for \(\rightarrow\) 1_1 , \(\rightarrow\) 1_2 ), while a few other events are recognized without ambiguity as Merge by all frameworks, such as (1_2,1_1) \(\rightarrow\) 2_0 or (1_5,1_0) \(\rightarrow\) 2_3 ).
However, we also find ambiguous cases in this dataset. Let us focus on one example, the event involving groups (0_15,0_0,0_1,1_0) : According to Asur et al. (2009), this event has no label. According to Greene et al., it is a merge from 0_0,0_1 into 1_0 , and 0_15 is a death. With our framework, 0_15,0_0,0_1 are classified as Ancestor s ( \(\mathcal =0.8\) ), while 1_0 -backward is Merge ( \(\mathcal =0.45\) ) and Expansion ( \(\mathcal =0.45\) ). Indeed, we see that this new group is composed of one-half of a perfect merge of those 3 predecessors, the other half being new entities. Through this example, we see that using a richer description is also useful even when group evolution is mostly stable.
Beyond focusing on individual events, our framework can be used to describe system-wide dynamics. Figure 8 details the evolution of events for each hour t, by computing the contribution of each event type as \(\sum _
From a backward perspective, most groups are born in the first hours (8:00–10:00), when students arrive at their classrooms and have the chance to connect. Conversely, group death in the forward perspective occurs at the end of days, when students leave the school.
Communities are mostly stable during class hours, as exemplified by the large Continuation areas between 9:00–12:00, and 14:00–17:00. However, some Merge , respectively Split events can also be observed during that period.
In the middle of the school day, students are primarily involved in Reorganization (backward) and Disassemble (forward) events, i.e., few students detach from large communities and form new groups, themselves composed of students from multiple groups. This can be interpreted as a lunchtime activity, in which students can meet peers from other classes. Indeed, we can validate this hypothesis by looking at the Attribute Entropy Change (cf. Appendix 3 for its definition), using class membership as an attribute. We observe an average \(\sim 25\%\) increase after Merge events, meaning that groups resulting from these events are more varied with respect to the contributing ones in the corresponding previous timestamp.
We can also observe a symmetric phenomenon, with Dispersion events occurring in the forward direction at the beginning of the lunch break, answered with Accumulation (backward) after the break. These event types are in the same color in the figures because they correspond to the same combination of facets. These events are characterized by important outflows. Indeed, one can observe that many students do not participate in the lunch break at school, which can explain this situation.
In fact, the full picture of a group’s transformations can be obtained by analyzing all of its event weights. For example, in Fig. 9, we show backward and forward event weights for group 2_7 . The backward event weights highlight a Merge -like event showing some traits of a Continuation (i.e., one larger contributing group), of an Offspring (due to the largest contributing group not coming in full), and of Reorganization (due to the low contribution of the smaller contributing groups). The forward event weights, instead, describe an event showing traits of Split — due to the separation into multiple, mostly equally-sized groups —- and Continuation because of the larger group moving to 3_9 .
In this paper, we introduced a framework to describe the temporal dynamics of groups by assessing their similarity to archetypal categories. This produces a flexible frame that removes the need for arbitrary thresholds while accurately representing the transformations at play at the same time. We have shown how this framework can be applied to the longitudinal analysis of temporal data, specifically in studying (i) the evolution of target groups, (ii) the evolution of the whole system in terms of its mesoscale dynamics, and (iii) how temporal granularity may impact observations on group transformations. We observed that, whatever the framework, identifying events with unstable dynamic groups seem doomed to fail, thus emphasizing the importance of smoothed dynamic clustering (Cazabet et al., 2020).
In this work, we focused on non-overlapping groups, as it remains the most common scenario both for clustering and community detection in graphs. The facets proposed could still work to characterize individual events in overlapping scenarios, however overlapping sets also have specificities that are not tackled in the present work. Other group specificities, such as periodically inactive groups (resurgences) or entities present in the system but belonging to no groups, or fuzzy groups, could be the focus on extensions of the present contribution. Another possible extension of our work would be to follow the work of Pereira et al. (2021) to define events adjusted for chance, i.e., if a group mostly continue in another group, but this would be expected in the case of random node assignment due to the group size, then we should normalize the scores obtained by the values expected due simply to chance.
Moreover, by introducing measures to quantify the change in the entities’ labels (see Definition 7 in Appendix 3), we also suggest that the relation between group structures and entities’ metadata could be explored further. For instance, this framework could be applied to the analysis of spatiotemporal clusters in human mobility data to understand whether differences in individual attributes are related to substantial differences in group mobility patterns. Another interesting applicative scenario could be the characterization of groups emerging from online social interactions to evaluate peer pressure effects, i.e., to measure the extent to which groups induce opinion change or, conversely, evaluate how opinion change drives group formation. To do so, however, one should account for time-changing attribute values, an aspect we did not cover in this work. Moving away from simply finding evolutive patterns in the data, this framework and its measures could be exploited to forecast both individual and group activity, e.g. using the proposed measures as input for a classification task.